Rabi oscillation and rotating frame

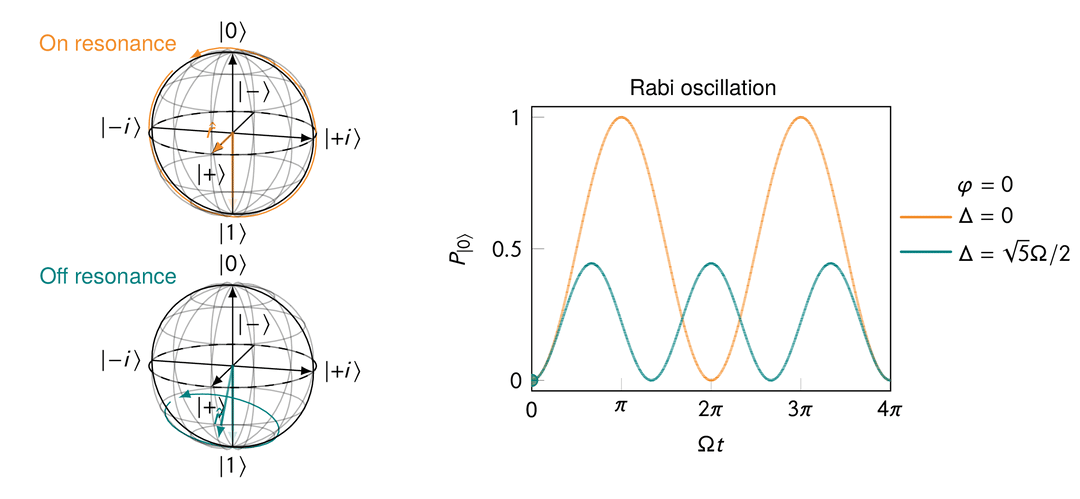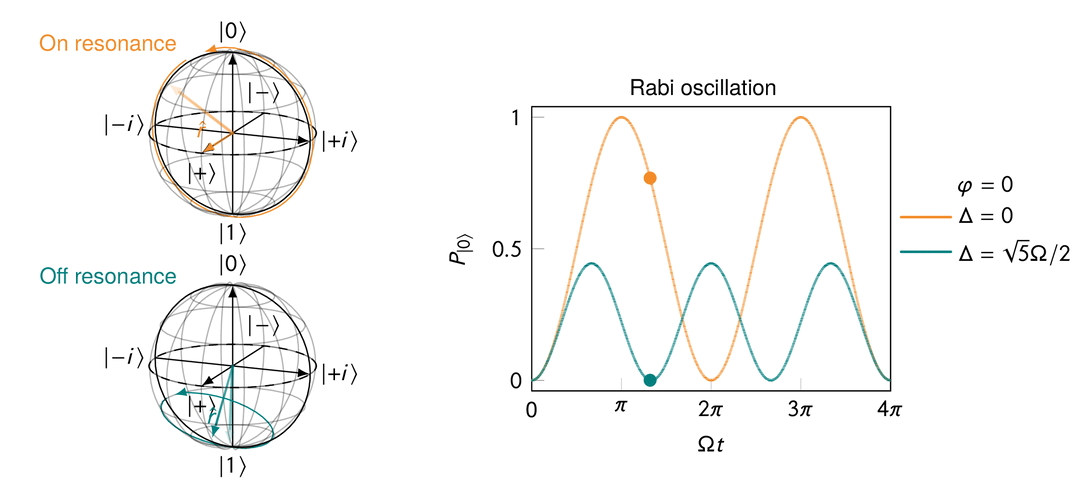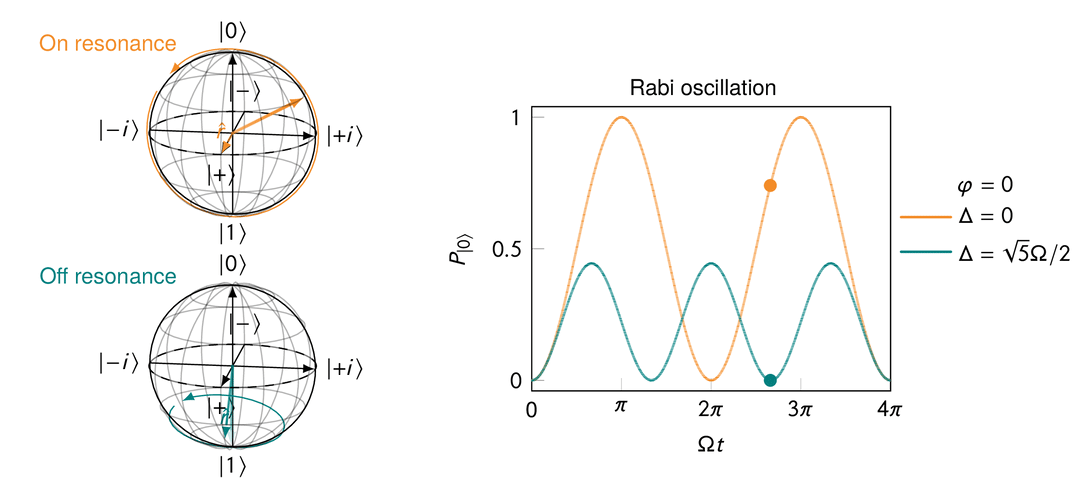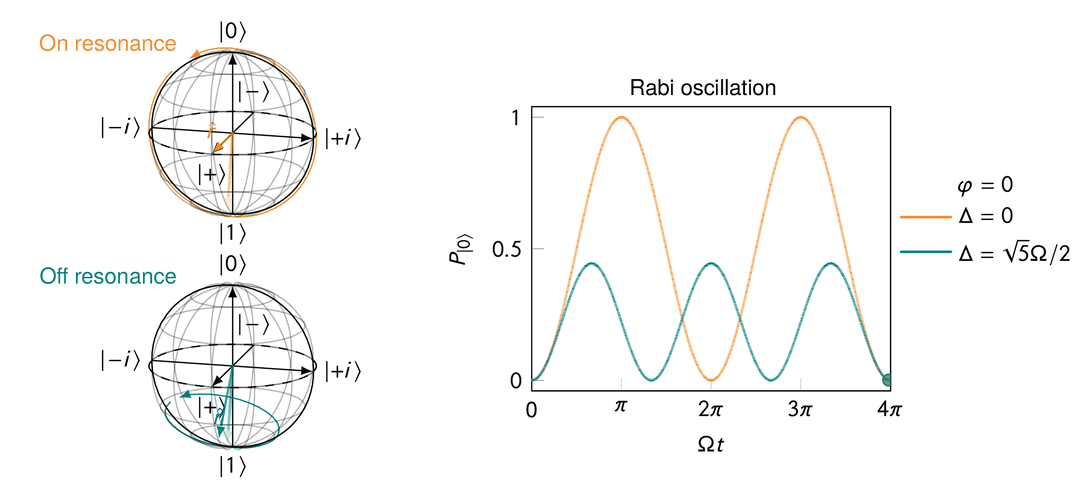
Rabi oscillation in the presence of a transverse magnetic field after a rotating frame transformation for both “on resonance” and “off resonance” cases.

Interaction of a qubit with an oscillating magnetic field

Hamiltonian for a general magnetic field

Consider a qubit whose magnetic moment is interacting with an external magnetic field. We write the Hamiltonian of such system as such:

where is the magnitude of the qubit’s magnetic moment, and the vector of Pauli matrices.

Static magnetic field with weakly oscillating transverse component

Now consider a static magnetic field along the -axis with magnitude and a weakly oscillating magnetic field along the plane with magnitude . The Hamiltonian then becomes:

where I have used and . Note that is the Rabi frequency. Unfortunately, eqn is time-dependent, which made it difficult to solve for the Schrödinger equation . In fact, there is no closed form solution available. To remedy this, we are going to re-write our Hamiltonian using the rotating frame transformation.

Going into the rotating frame

Rewriting the Hamiltonian for convenience

Before going into the rotating frame, we can rewrite eqn by noting that and :

where we have also introduced for convenience. As we move on from this, you will see that the rewritten Hamiltonian is much easier to work with when going into the rotating frame.

Hamiltonian in the rotating frame

To obtain the Hamiltonian in the rotating frame about the -axis at frequency , we introduce the following evolution operator and the formula . After working this formula out, you should get:

which is time-independent! It is now possible to determine via a closed form solution what our initial input state becomes after time evolution due to our new Hamiltonian:

Time evolution due to the Hamiltonian

On resonance, i.e., , our initial state oscillates between and :

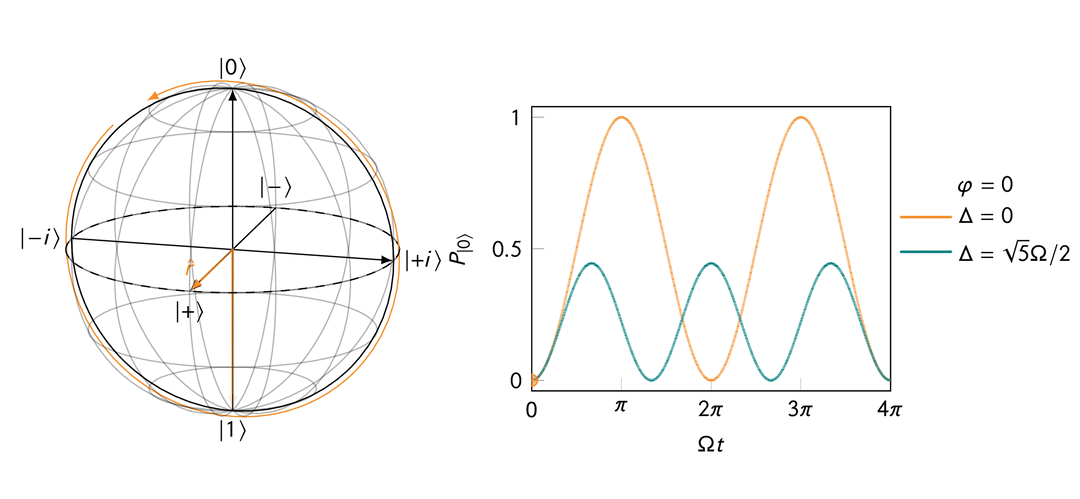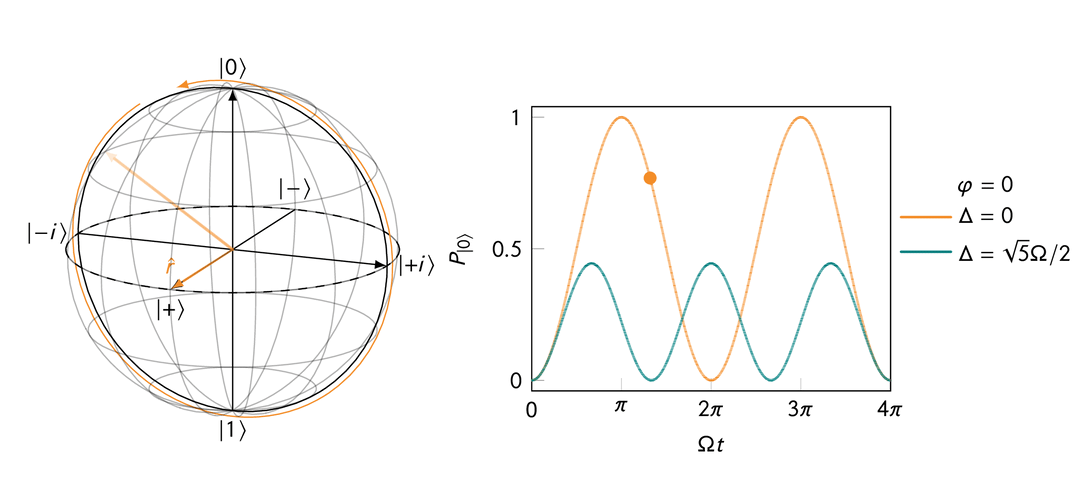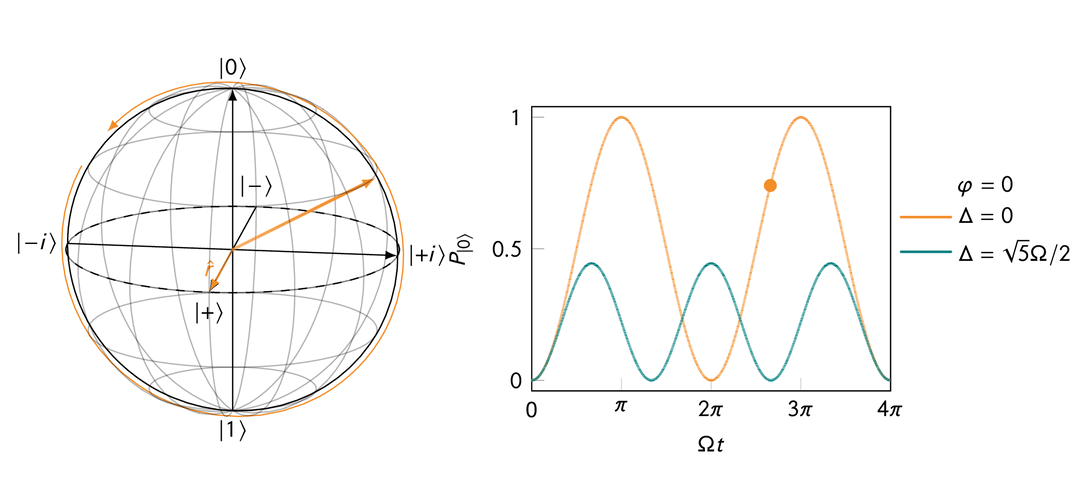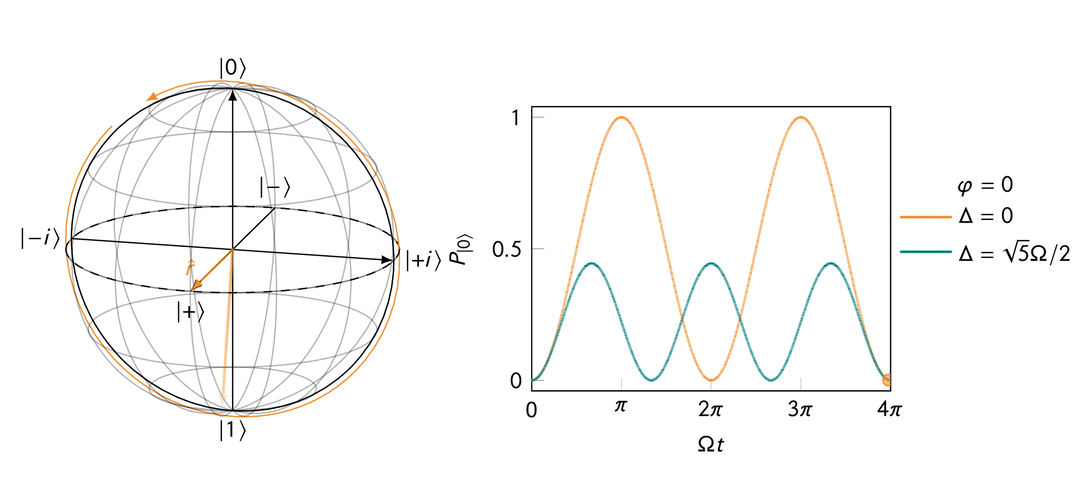
This makes sense because when , the term goes to zero in eqn resulting in a rotation about some axis along the -plane. Since , only the term survives, hence the axis of rotation is along the -axis.

When off resonance, i.e., , our state no longer oscillates in such a way that anymore due to the non-zero term:

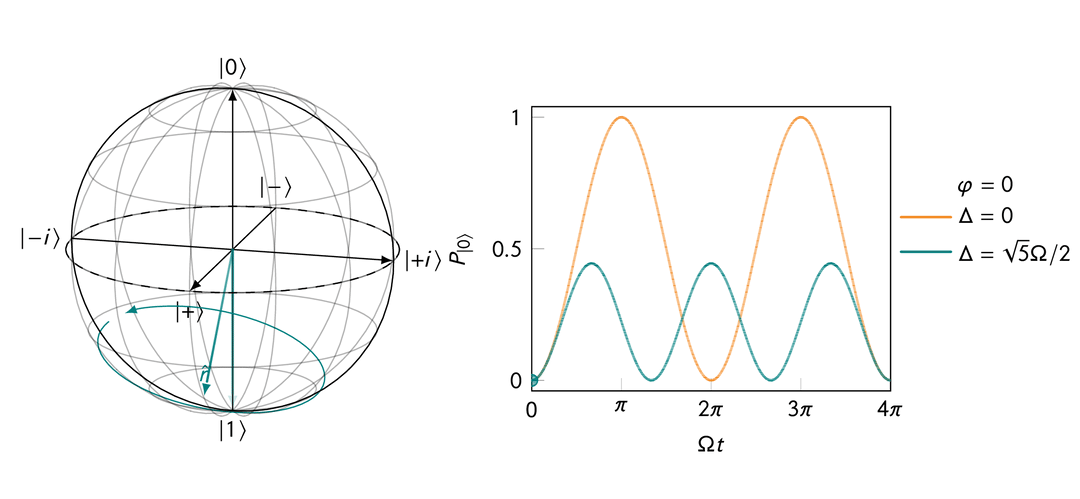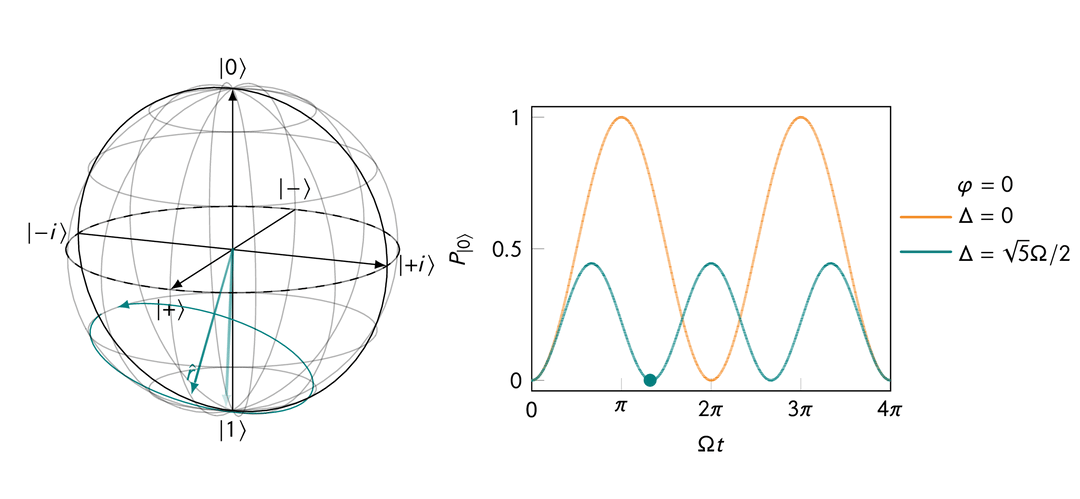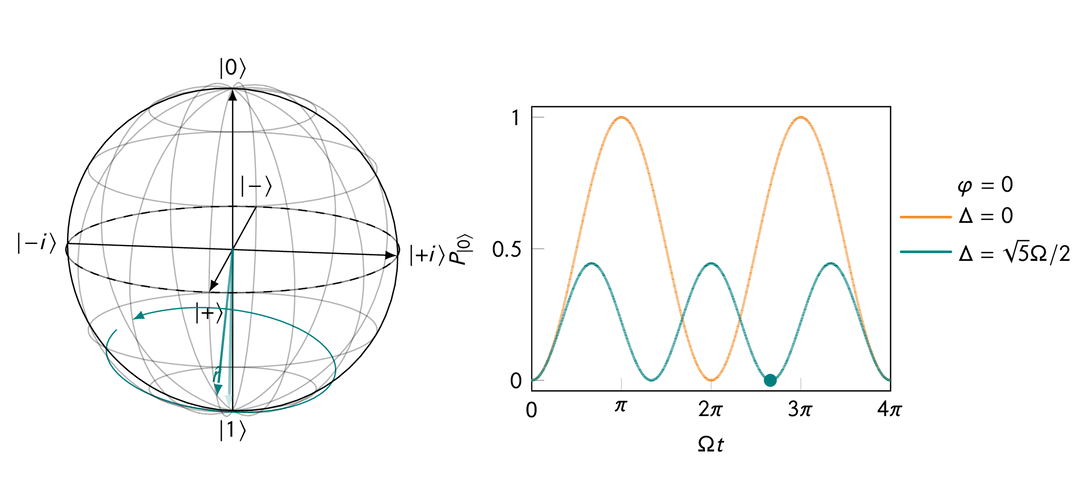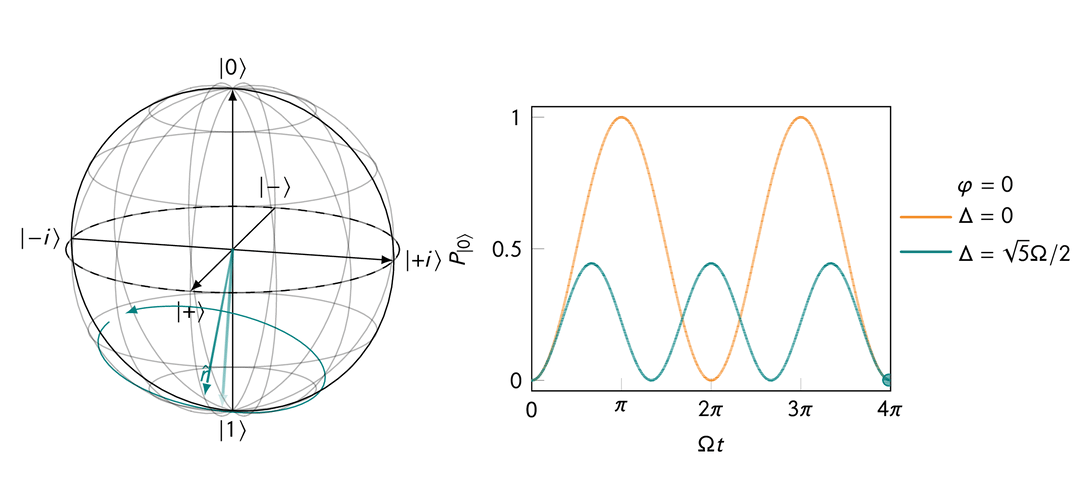
If you apply a -pulse, then , which results in rotation about the -axis instead:

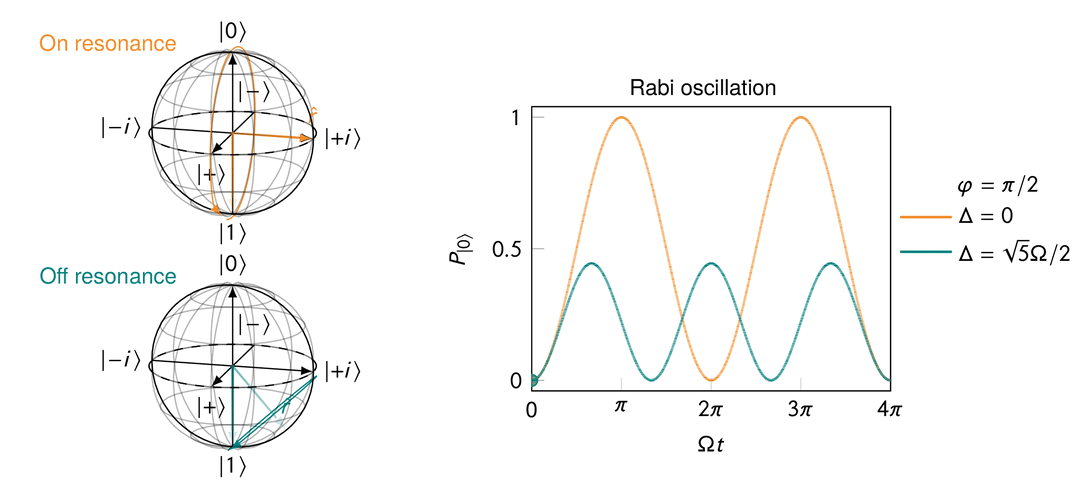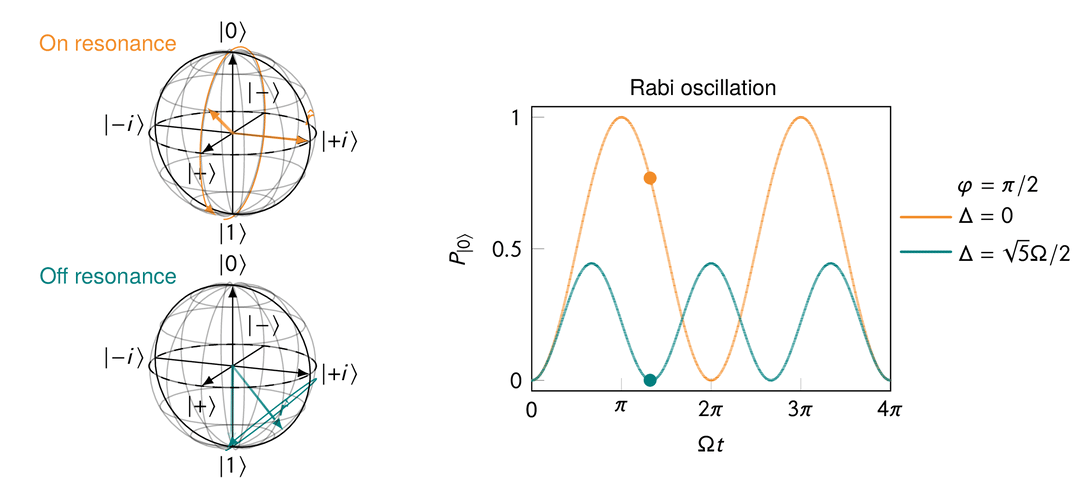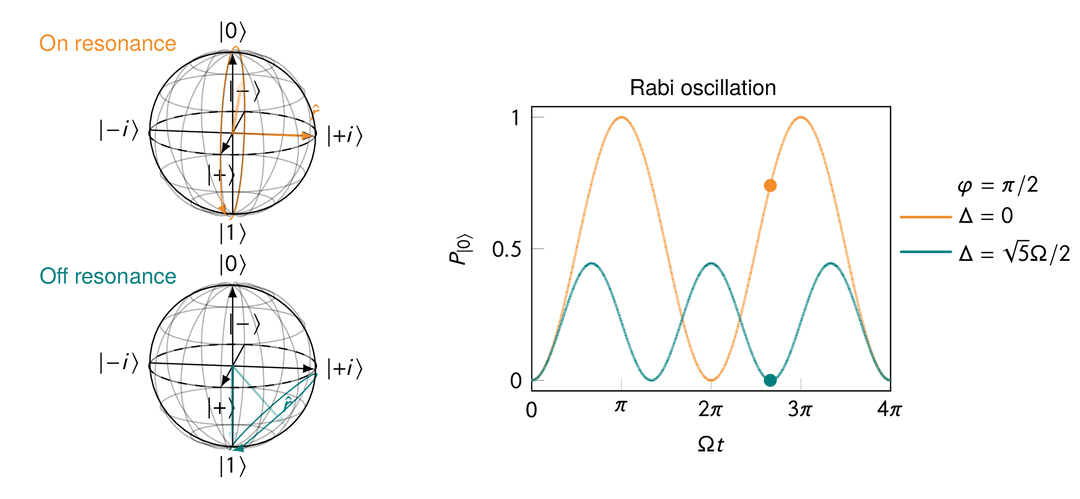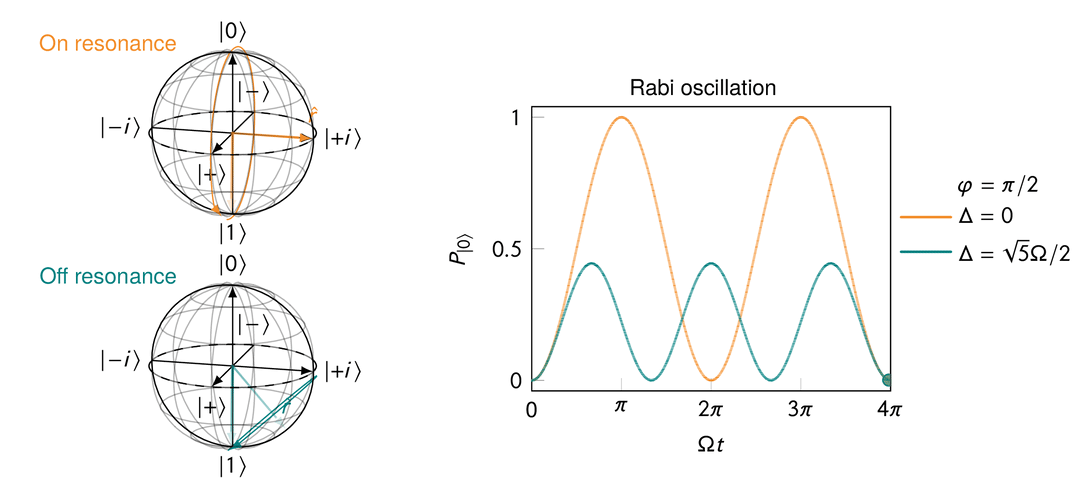
In quantum computing, Rabi oscillations are crucial since they provide the basic means of manipulating the state of qubits to perform any meaningful computation.

Appendix

Derivation of the Hamiltonian in a rotating frame

Therefore, , where your rotating frame is dictated by your choice of .